Next: Example: Motion in a Up: Hamiltonian Mechanics Previous: Example: Particle in 3D Contents
Consider a
pendulum bob of mass
![]() hanging from the ceiling by a string of length
hanging from the ceiling by a string of length
![]() and free to move in two dimensions like the Foucault pendulum.
The free variables are
and free to move in two dimensions like the Foucault pendulum.
The free variables are
![]() and
and
![]() of spherical coordinates and the energies are given by
of spherical coordinates and the energies are given by
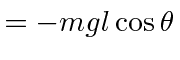 |
||
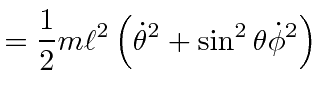 |
||
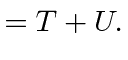 |
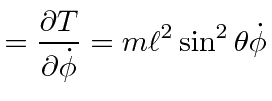 |
||
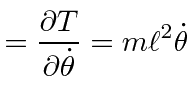 |
||
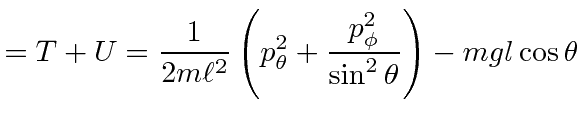 |
||
 |
||
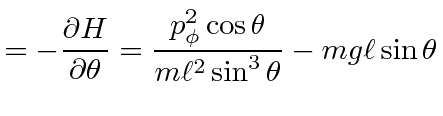 |
Jim Branson 2012-10-21