Next: Covariant Electricity and Magnetism Up: Special Relativity Previous: Compton Scattering Contents
The basis for Special Relativity is that the laws of physics are independent of which inertial coordinate system we write them in. We wish to write equations in terms of scalars, 4-vectors, and tensors, with both sides of the equation transforming the same way under rotations and boosts. Such equations are said to be covariant, because both sides of the equation transform in the same standard way. The Lagrangian is based on the principle of least Action. The Action as we know it so far is clearly not a vector or a tensor so our obvious choice is to make it a scalar. Our definition of the Action so far is.
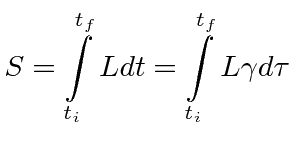
For a particle, the mass is the only scalar we can use. Clearly this is not related to external potential applied to the particle.
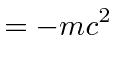 |
||
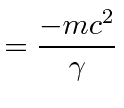 |
||
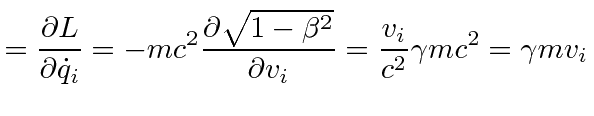 |
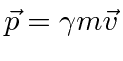 indicating that we have picked the right kinetic term for the Lagrangian.
indicating that we have picked the right kinetic term for the Lagrangian.
The (velocity independent) potential can be subtracted.
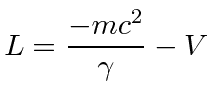 |
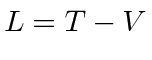 in nonrelativistic problems.
To have fully relativistic problems we need to have potentials, for example, that are relativistically correct.
We will take a look at the relativistic equations of electromagnetism, but this is really beyond the scope of this course.
In field theory, there will be scalar interaction terms in the Lagrangian,
like the interaction between the electric current due to particles with the vector potential,
a dot product between 4-vectors.
in nonrelativistic problems.
To have fully relativistic problems we need to have potentials, for example, that are relativistically correct.
We will take a look at the relativistic equations of electromagnetism, but this is really beyond the scope of this course.
In field theory, there will be scalar interaction terms in the Lagrangian,
like the interaction between the electric current due to particles with the vector potential,
a dot product between 4-vectors.
The Hamiltonian can be computed from the Lagrangian.
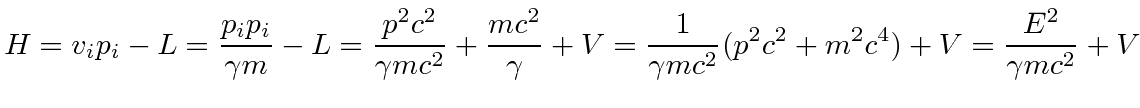
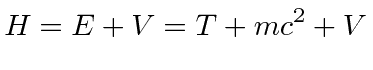
It is quite interesting to look at this Action which is to be minimized in Minkowski space and to try to formulate the principle of least Action in a covariant way.

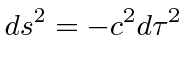
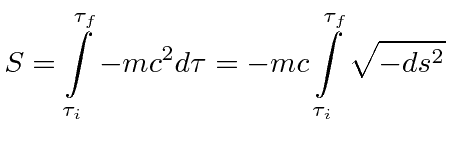
We may take this back to an integral over proper time.
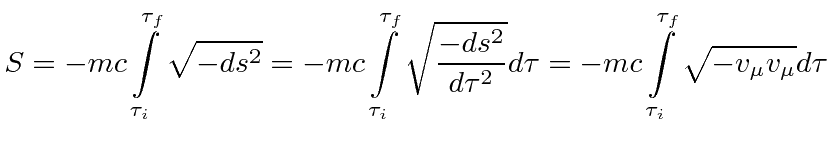
Jim Branson 2012-10-21