Next: The 4D Gradient Operator Up: Special Relativity Previous: The Force 4-Vector Contents
We started with the position vector in Minkowski space.
 |
 |
The difference between spacetime points for a single particle is an important case. We use the dot product of this difference with itself.
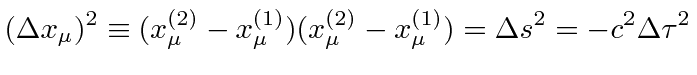 |
We define the velocity 4-vector with the equation.
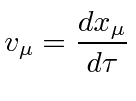 |
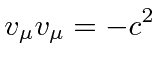 |
We define the momentum 4-vector with.
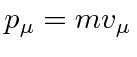 |
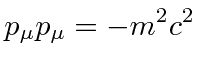 |
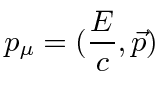 |
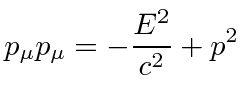 |
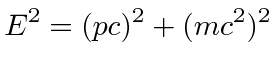 |
The dot product of the momentum 4-vector and the position 4-vector
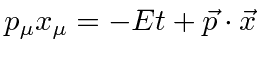
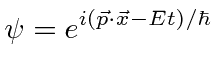
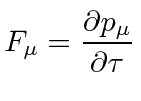 |
Jim Branson 2012-10-21