Next: The Force 4-Vector Up: The Momentum-Energy 4-Vector Previous: The Momentum-Energy 4-Vector Contents
The problem we have is
how to take a time derivative if the time is the component of a 4-vector.
We need some kind of
scalar time to make sense of the equations we know and love.
A well defined time, that does not need to be transformed, is the
time in the rest frame of the particle.
We call this the
proper time
![]() .
We will make use of it here, but later just try to rewrite our equations so that they are
covariant in 4 dimensions.
.
We will make use of it here, but later just try to rewrite our equations so that they are
covariant in 4 dimensions.
The velocity 4-vector can be defined as.

 |
We can dot the velocity 4-vector into itself.

To be consistent with non-relativistic equations we will define the momentum.

If we identify the time component as above,
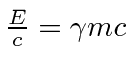 , we have the relation
, we have the relation

A crucial test of this ``derived'' 4-vector is whether it gives the right physics in the non-relativistic limit. We did have some choice to make when inserting the energy into the momentum 4-vector. Start with the energy equation from above.
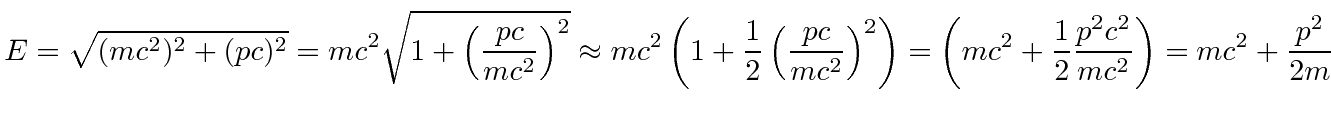 |
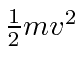 .
Normally, we ignore the rest energy as being unchangeable.
It does change in nuclear interactions for example.
.
Normally, we ignore the rest energy as being unchangeable.
It does change in nuclear interactions for example.
Jim Branson 2012-10-21