Next: The Momentum-Energy 4-Vector Up: Special Relativity Previous: A Boost in an Contents
We have derived the velocity addition formula using two Lorentz transformations (in the same direction) and rapidity.
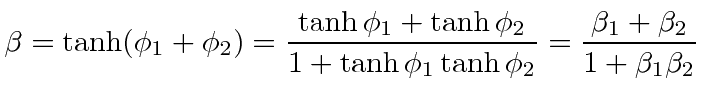
We can also compute this in terms of the usual
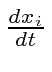 going from one frame in which an object is moving
to a frame boosted along the
going from one frame in which an object is moving
to a frame boosted along the
![]() direction.
(This should give the same result as above if the particle is moving in the
direction.
(This should give the same result as above if the particle is moving in the
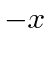 direction.)
direction.)
Let the velocity in the original system be
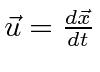 .
.
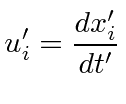 |
||
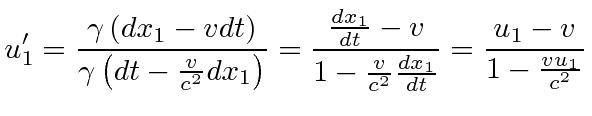 |
||
 |
||
 |
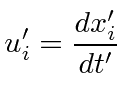
|
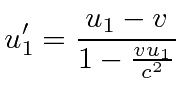
|
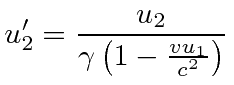
|
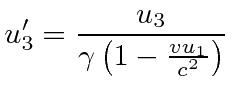 |
Jim Branson 2012-10-21