Next: Hyperbolic Function Identities Up: Special Relativity Previous: Symmetry Transformations in Minkowski Contents
Minkowski space is called a
hyperbolic geometry.
Clearly the time coordinate is not treated the same as the space coordinates.
We will find that when space and time coordinates are mixed in a transformation,
that we use the
hyperbolic functions
![]() and
and
![]() instead of
instead of
![]() and
and
![]() .
They are very symmetrically defined.
.
They are very symmetrically defined.
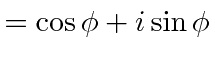 |
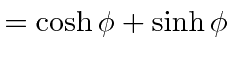 |
|||
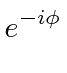 |
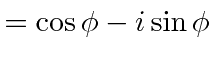 |
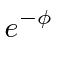 |
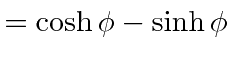 |
|
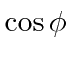 |
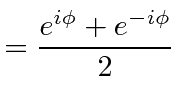 |
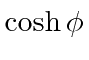 |
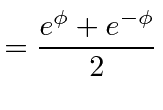 |
|
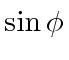 |
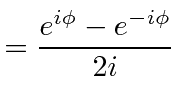 |
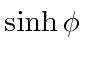 |
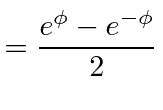 |
|
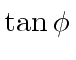 |
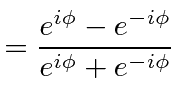 |
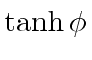 |
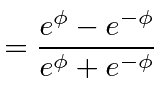 |