Next: The Tides Up: Noninertial Frames of Reference Previous: Calculating the Effective Force Contents
The earth rotates with and
angular frequency of
about1
![]() radians per (sidereal) day.
The
axis of the earth's rotation goes through the north and south poles of the earth.
The direction of
radians per (sidereal) day.
The
axis of the earth's rotation goes through the north and south poles of the earth.
The direction of
![]() goes from south to north pole.
The axis is at about
goes from south to north pole.
The axis is at about
![]() radians from the plane of the earth's orbit, causing the observed seasons.
radians from the plane of the earth's orbit, causing the observed seasons.
The primary effect of the centrifugal force is to change the magnitude and direction of the apparent acceleration of gravity near the earth.

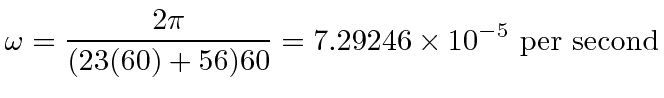

Lets analyze the
effect of the centrifugal acceleration at all latitudes,
under the assumption that the earth is spherical.
At non-zero latitude the first cross product
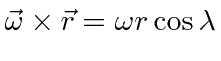 ,
so the magnitude of the centrifugal acceleration is
,
so the magnitude of the centrifugal acceleration is
![]() and the direction is
outward perpendicular to the axis of rotation.
In the local coordinate system, this means that there is a radial component of the centrifugal
acceleration which reduces the effective
and the direction is
outward perpendicular to the axis of rotation.
In the local coordinate system, this means that there is a radial component of the centrifugal
acceleration which reduces the effective
![]()
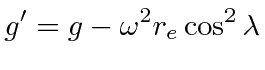
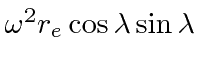 .
This component has very small effect on the magnitude of
.
This component has very small effect on the magnitude of
Of course if the earth were a fluid of uniform density, it would take on a shape
such that the effective
![]() would be normal to the surface of the fluid.
Newton calculated that this would make radius of the earth at the equator
one part in 230 larger than the radius at the poles.
The earth would take on the shape of an oblate spheroid.
With much of the earth molten, it is easily deformable into this shape, however,
the density is much larger at small radius than it is at the surface.
Recent measurements give a somewhat smaller effect of one part in 298.25642.
The oblate spheroid is the baseline for measurements of the earths shape.
Gravity actually depends on the local mass density of the earth but
the baseline model of
would be normal to the surface of the fluid.
Newton calculated that this would make radius of the earth at the equator
one part in 230 larger than the radius at the poles.
The earth would take on the shape of an oblate spheroid.
With much of the earth molten, it is easily deformable into this shape, however,
the density is much larger at small radius than it is at the surface.
Recent measurements give a somewhat smaller effect of one part in 298.25642.
The oblate spheroid is the baseline for measurements of the earths shape.
Gravity actually depends on the local mass density of the earth but
the baseline model of
![]() as a function of latitude is approximately.
as a function of latitude is approximately.
![\bgroup\color{black}$\displaystyle g=9.7803267714\left[{1+0.00193185138639\sin^2\lambda\over\sqrt{1-0.00669437999013\sin^2\lambda}}\right] $\egroup](img239.png)
Besides the forces due to rotation, there are some effective forces due to the acceleration of the coordinate system. The earth is essentially in free fall in the gravitational field of the moon and the sun, so that the net force of gravity is exactly canceled by the acceleration of the earth. Only the net force is canceled. Since the effective force varies with position on the earth, there are tidal forces that cause the oceans to rise and fall.
Jim Branson 2012-10-21