Next: Lorentz Transformation of the Up: Covariant Electricity and Magnetism Previous: Rationalized Heaviside-Lorentz Units Contents
The transformation of electric and magnetic fields under a Lorentz boost we established even before Einstein developed the theory of relativity. We know that E-fields can transform into B-fields and vice versa. For example, a point charge at rest gives an Electric field. If we boost to a frame in which the charge is moving, there is an Electric and a Magnetic field. This means that the E-field cannot be a Lorentz vector. We need to put the Electric and Magnetic fields together into one (tensor) object to properly handle Lorentz transformations and to write our equations in a covariant way.
The simplest way and the correct way to do this is to make the Electric and Magnetic fields components of a rank 2 (antisymmetric) tensor.
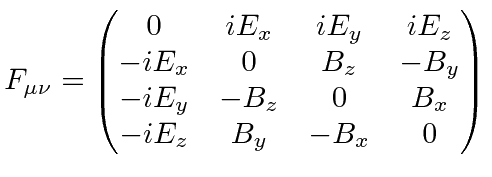 |
The fields can simply be written in terms of the
vector potential, (which is a Lorentz vector)
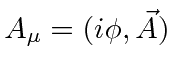 .
.
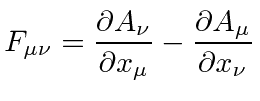 |
Note that this is automatically antisymmetric under the interchange of the indices.
As before, the
first two (sourceless) Maxwell equations are automatically satisfied for fields
derived from a vector potential.
We may write the
other two Maxwell equations in terms of the 4-vector
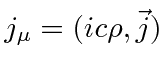 .
.
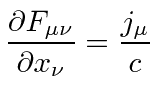 |
Which is why the T-shirt given to every MIT freshman when they take Electricity and Magnetism should say
``... and God said
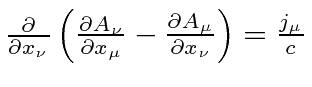 and there was light.''
and there was light.''
Of course he or she hadn't yet quantized the theory in that statement.
For some peace of mind, lets verify a few terms in the equations. Clearly all the diagonal terms in the field tensor are zero by antisymmetry. Lets take some example off-diagonal terms in the field tensor, checking the (old) definition of the fields in terms of the potential.
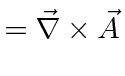 |
||
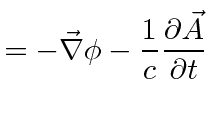 |
||
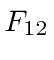 |
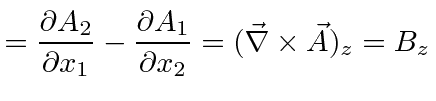 |
|
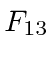 |
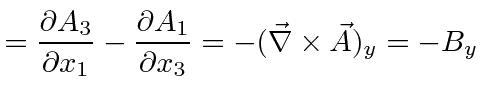 |
|
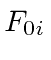 |
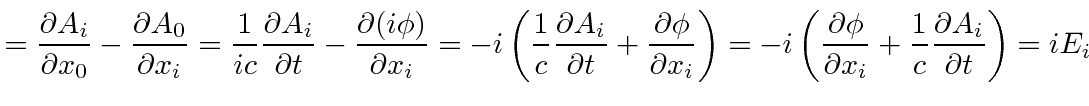 |
Lets also check what the Maxwell equation says for the last row in the tensor.
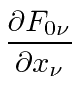 |
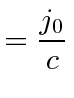 |
|
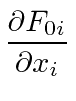 |
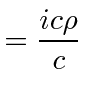 |
|
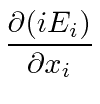 |
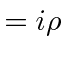 |
|
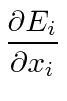 |
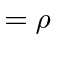 |
|
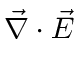 |
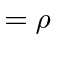 |
Jim Branson 2012-10-21