Next: Deriving the Momentum-Energy 4-Vector Up: Special Relativity Previous: Velocity Addition Contents
It is obviously important it determine how Energy and Momentum transform in Special Relativity. A reasonable guess is that momentum is a 3-vector conjugate to position, so we need to find what the fourth component is to make a 4-vector. We again have the problem of the speed of light not being equal to one in our units. The answer, which we will derive below, is that the Momentum-Energy 4-vector is
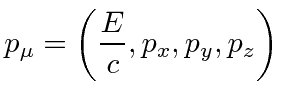 |
The dot product with itself is
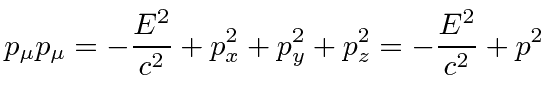
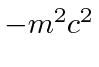 , and we get the equation.
, and we get the equation.
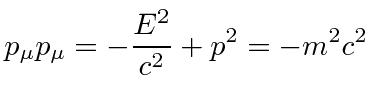
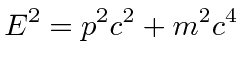
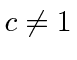 is vexing but we get the
basic Energy equation of Special relativity.
is vexing but we get the
basic Energy equation of Special relativity.
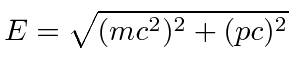 |
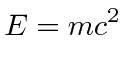
Of course any 4-vector transforms like a 4-vector so we have the transformation equations for momentum
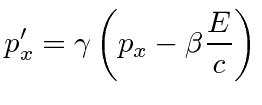
|
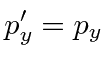
|
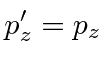
|
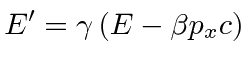 |
Lets start in the rest frame and do a transformation.
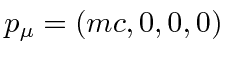 |
||
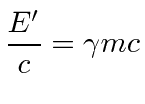 |
||
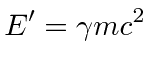 |
||
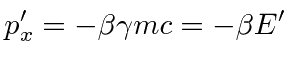 |
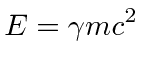 |
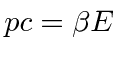 |